¿Alguna vez te has preguntado cómo trazar una parábola de manera precisa? ¡No busques más! Con nuestra calculadora de parábolas, podrás resolver fácilmente ecuaciones cuadráticas y graficar rápidamente las curvas de estas formas geométricas tan fascinantes. Descubre cómo calcular vértices, focos y directrices con tan solo unos clics. ¡Sigue leyendo para aprender cómo dominar el arte de las parábolas!

Calculadora de Parábolas

Coeficiente a:


Coeficiente b:


Coeficiente c:


Calcular

Calculadora de Parábola: Herramienta para Analizar y Graficar Parábolas

Cuando te encuentres con una fórmula cuadrática que deseas analizar, encontrarás que esta calculadora de parábola es la herramienta perfecta para ti. No solo te brindará la ecuación de la parábola en la forma estándar y en la forma del vértice, sino que también calculará el vértice de la parábola, el foco y la directriz para ti.

¿Qué es una Parábola?

Una parábola es una curva simétrica en forma de U. Su propiedad principal es que cada punto que se encuentra en la parábola está equidistante de un punto específico, llamado el foco de una parábola, y una línea, llamada su directriz. También es la curva que corresponde a las ecuaciones cuadráticas.

Fórmula Estándar de una Parábola

La forma estándar de una ecuación cuadrática es y = ax² + bx + c. Puedes usar esta calculadora para transformar esa ecuación en la forma del vértice, que te permite encontrar los puntos importantes de la parábola: su vértice y su foco.

Fórmula del Vértice de la Parábola

La ecuación de la parábola en su forma del vértice es y = a(x – h)² + k, donde:

• a — Mismo coeficiente que en la forma estándar;
• h — Coordenada x del vértice de la parábola; y
• k — Coordenada y del vértice de la parábola.

Calcula los valores de h y k utilizando las siguientes ecuaciones:

h = – b/(2a)

k = c – b²/(4a)

Fórmula del Foco y Directriz de la Parábola

La calculadora de la forma del vértice de la parábola también encuentra el foco y la directriz de la parábola. Todo lo que tienes que hacer es usar las siguientes ecuaciones:

• Coordenada x del Foco: x₀ = – b/(2a);
• Coordenada y del Foco: y₀ = c – (b² – 1)/(4a); y
• Ecuación de la Directriz: y = c – (b² + 1)/(4a).

Ejemplo de Cálculo

Si asumimos que la ecuación es y = 2x² + 3x – 4, lo que significa que a = 2, b = 3 y c = -4:

Calcula las coordenadas del vértice:

h = -3/4 = -0.75

k = -4 – 9/8 = -5.125

Encuentra las coordenadas del foco de la parábola:

x₀ = -0.75

y₀ = -5

Encuentra la directriz de la parábola:

y = -5.25

Conclusión

La calculadora de parábola es una herramienta útil para analizar y graficar parábolas con facilidad. ¡Empieza a utilizarla y descubre más sobre las propiedades de las parábolas!

Preguntas Frecuentes sobre la Calculadora de Parábola

¿Qué es una parábola?

Una parábola es una curva en dos dimensiones que es simétrica y se forma a partir de un punto llamado foco y una línea recta llamada directriz. Es una forma común en matemáticas y física, y se utiliza en una variedad de aplicaciones.

¿Qué es una calculadora de parábola?

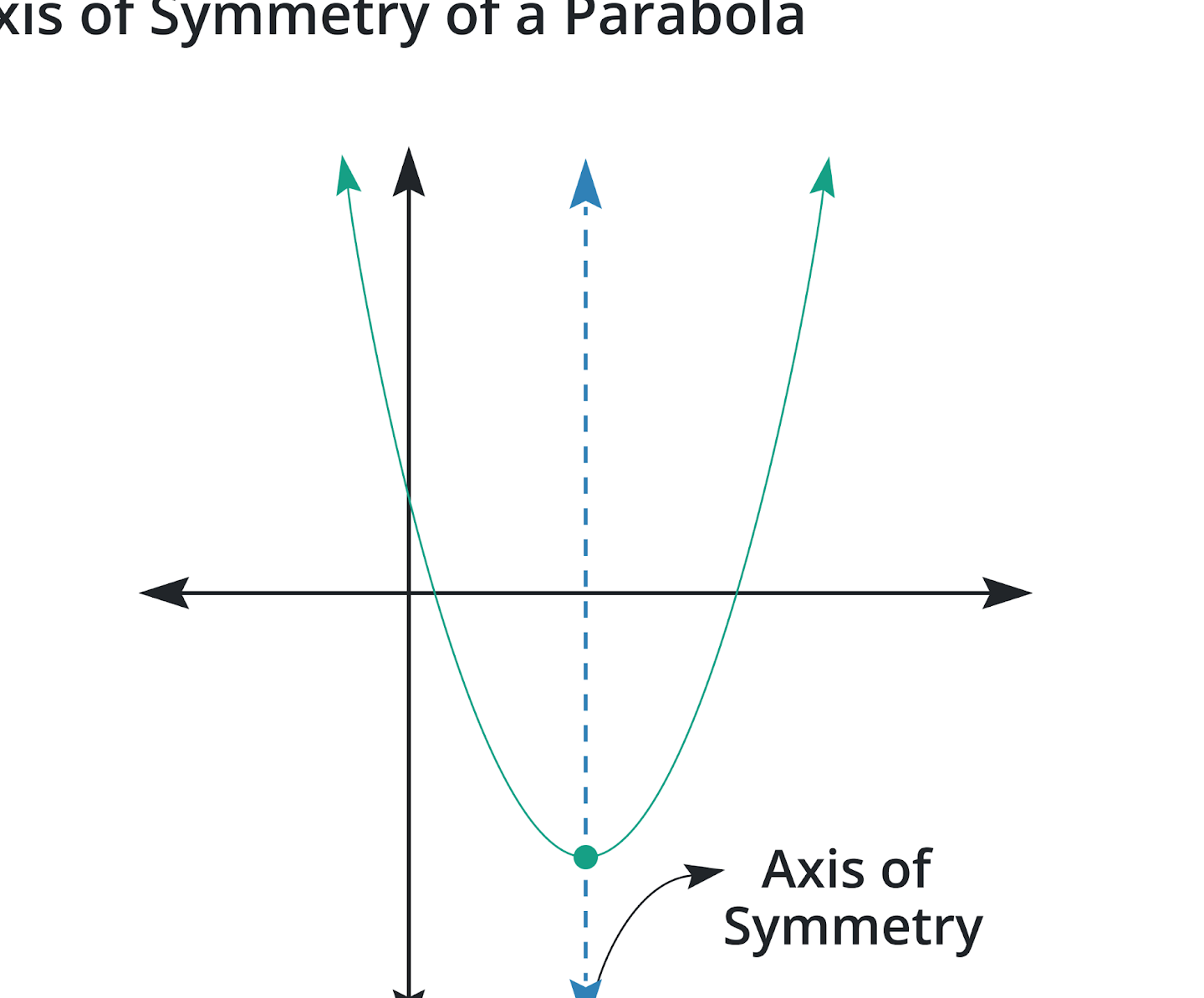
Una calculadora de parábola es una herramienta en línea que te permite introducir los coeficientes de una ecuación cuadrática y te proporciona información sobre la parábola resultante, como la ubicación del vértice, el eje de simetría, los puntos de intersección con los ejes, y más.

¿Cómo se utiliza una calculadora de parábola?

Para utilizar una calculadora de parábola, simplemente debes introducir los coeficientes de la ecuación cuadrática en los campos designados y hacer clic en el botón de cálculo. La calculadora te mostrará los resultados de forma rápida y precisa.

¿Cuáles son los beneficios de utilizar una calculadora de parábola?

• Facilidad y rapidez para obtener información sobre una parábola.
• Ayuda a comprender mejor las propiedades y características de las parábolas.
• Permite verificar y graficar ecuaciones cuadráticas de manera sencilla.

Consejos prácticos para utilizar una calculadora de parábola

Para obtener resultados precisos, asegúrate de introducir correctamente los coeficientes en la calculadora. También es útil revisar los resultados obtenidos para tener una mejor comprensión de la parábola en cuestión.

Ejemplo de uso de una calculadora de parábola

Imagina que tienes la ecuación cuadrática y = x^2 + 4x + 4. Al introducir los coeficientes en la calculadora de parábola, obtendrías información como el vértice en (-2, 0) y el eje de simetría en x = -2. Esto te permite visualizar mejor la forma y la posición de la parábola en cuestión.

¡Esperamos que esta información te haya sido útil para comprender mejor qué es y cómo utilizar una calculadora de parábola!

[automatic_youtube_gallery type=»search» search=»Calculadora de Parábolas» limit=»1″]